Monday, June 21, 2010
Sunday, June 20, 2010
Albert Einstein
| Albert Einstein | |
|---|---|
 Albert Einstein, 1921 | |
| Born | 14 March 1879 Ulm, Kingdom of Württemberg, German Empire |
| Died | 18 April 1955 (aged 76) Princeton, New Jersey, USA |
| Resting place | Grounds of the Institute for Advanced Study, Princeton, New Jersey. |
| Residence | Germany, Italy, Switzerland, USA |
| Ethnicity | German Jewish |
| Citizenship |
|
| Alma mater | |
| Known for | |
| Spouse(s) |
|
| Awards |
|
Signature  | |
Physics Experiment
Experiment is the step in the scientific method that arbitrates between competing models or hypotheses.[1][2] Experimentation is also used to test existing theories or new hypotheses in order to support them or disprove them.[3][4] An experiment or test can be carried out using the scientific method to answer a question or investigate a problem. First an observation is made. Then a question is asked, or a problem arises. Next, a hypothesis is formed. Then experiment is used to test that hypothesis. The results are analyzed, a conclusion is drawn, sometimes a theory is formed, and results are communicated through research papers.
A good experiment usually tests a hypothesis. However, an experiment may also test a question or test previous results.
- Replication of results is "a standard procedure in the validation of any scientific discovery." [4]
- "Science was long protected from fraud by a built-in safety mechanism: to be generally accepted, experiments must be repeatable by others." [5]
It is important that one knows all factors in an experiment. It is also important that the results are as accurate as possible. If an experiment is carefully conducted, the results usually either support or disprove the hypothesis. An experiment can never "prove" a hypothesis, it can only add support. However, one repeatable experiment that provides a counterexample can disprove a theory or hypothesis. An experiment must also control the possible confounding factors -- any factors that would mar the accuracy or repeatability of the experiment or the ability to interpret the results.
Types of experiments
[edit] Controlled experiments
An experiment or test or show can be carried out by using the scientific method. The steps are make an observation, ask a question, form a hypothesis, test the hypothesis, analyze the results, draw a conclusion, and communicate results. The reason a hypothesis is tested is so that it can be confirmed, denied, or refined, with the knowledge currently available. The test has one variable. The control is the regular group and experimental is the group with the variable added to it.
To demonstrate a cause and effect hypothesis, an experiment must often show that, for example, a phenomenon occurs after a certain treatment is given to a subject, and that the phenomenon does not occur in the absence of the treatment. (See Baconian method.)
A controlled experiment generally compares the results obtained from an experimental sample against a control sample, which is practically identical to the experimental sample except for the one aspect whose effect is being tested (the independent variable). A good example would be a drug trial. The sample or group receiving the drug would be the experimental one; and the one receiving the placebo would be the control one. In many laboratory experiments it is good practice to have several replicate samples for the test being performed and have both a positive control and a negative control. The results from replicate samples can often be averaged, or if one of the replicates is obviously inconsistent with the results from the other samples, it can be discarded as being the result of an experimental error (some step of the test procedure may have been mistakenly omitted for that sample). Most often, tests are done in duplicate or triplicate. A positive control is a procedure that is very similar to the actual experimental test but which is known from previous experience to give a positive result. A negative control is known to give a negative result. The positive control confirms that the basic conditions of the experiment were able to produce a positive result, even if none of the actual experimental samples produce a positive result. The negative control demonstrates the base-line result obtained when a test does not produce a measurable positive result; often the value of the negative control is treated as a "background" value to be subtracted from the test sample results. Sometimes the positive control takes the quadrant of a standard curve.
An example that is often used in teaching laboratories is a controlled protein assay. Students might be given a fluid sample containing an unknown (to the student) amount of protein. It is their job to correctly perform a controlled experiment in which they determine the concentration of protein in fluid sample (usually called the "unknown sample"). The teaching lab would be equipped with a protein standard solution with a known protein concentration. Students could make several positive control samples containing various dilutions of the protein standard. Negative control samples would contain all of the reagents for the protein assay but no protein. In this example, all samples are performed in duplicate. The assay is a colorimetric assay in which a spectrophotometer can measure the amount of protein in samples by detecting a colored complex formed by the interaction of protein molecules and molecules of an added dye. In the illustration, the results for the diluted test samples can be compared to the results of the standard curve (the blue line in the illustration) in order to determine an estimate of the amount of protein in the unknown sample.
Controlled experiments can be performed when it is difficult to exactly control all the conditions in an experiment. In this case, the experiment begins by creating two or more sample groups that are probabilistically equivalent, which means that measurements of traits should be similar among the groups and that the groups should respond in the same manner if given the same treatment. This equivalency is determined by statistical methods that take into account the amount of variation between individuals and the number of individuals in each group. In fields such as microbiology and chemistry, where there is very little variation between individuals and the group size is easily in the millions, these statistical methods are often bypassed and simply splitting a solution into equal parts is assumed to produce identical sample groups.
Once equivalent groups have been formed, the experimenter tries to treat them identically except for the one variable that he or she wishes to isolate. Human experimentation requires special safeguards against outside variables such as the placebo effect. Such experiments are generally double blind, meaning that neither the volunteer nor the researcher knows which individuals are in the control group or the experimental group until after all of the data have been collected. This ensures that any effects on the volunteer are due to the treatment itself and are not a response to the knowledge that he is being treated.
In human experiments, a subject (person) may be given a stimulus to which he or she should respond. The goal of the experiment is to measure the response to a given stimulus by a test method.
[edit] Natural experiments
A natural experiment is an observational study in which the assignment of treatments to subjects has been haphazard: That is, the assignment of treatments to subjects has not been made by experimenters (and certainly not by randomization). Natural experiments are most useful when there has been a clearly defined and large change in the treatment (or exposure) to a clearly defined subpopulation, so that changes in responses may be plausibly attributed to the change in treatments (or exposure). Natural experiments are considered for study designs whenever controlled experimentation is difficult, such as in epidemiology and economics.
One of the most famous natural experiments was the 1854 Broad Street cholera outbreak in London, England. On 31 August 1854, a major outbreak of cholera struck Soho. Over the next three days 127 people near Broad Street died. By the end of the outbreak 616 people died. The physician John Snow identified the source of the outbreak as the nearest public water pump, which he identified using a a map of deaths and illness. In this example, Snow discovered a strong association between the use of the water and deaths and illnesses due to cholera. Snow found that the water company (the Southwark and Vauxhall Company) that supplied water to districts with high attack rates obtained the water from the Thames downstream from where raw sewage was discharged into the river. By contrast, districts that were supplied water by the Lambeth Company, which obtained water upstream from the points of sewage discharge, had low attack rates. The water supply in mid-Nineteenth Century London wsa not developed by scientists studying cholera, and so exposure to this well may be considered a haphazard event. [6] Therefore, this exposure has been recognized as being a natural experiment. [7][8]
[edit] Field experiments
Field experiments are so named in order to draw a contrast with laboratory experiments. Often used in the social sciences, and especially in economic analyses of education and health interventions, field experiments have the advantage that outcomes are observed in a natural setting rather than in a contrived laboratory environment. However, like natural experiments, field experiments suffer from the possibility of contamination: experimental conditions can be controlled with more precision and certainty in the lab.
[edit] History
[edit] Francis Bacon
Francis Bacon was an English philosopher and scientist in the 1600s and an early and influential supporter of experimental science. He disagreed with the method of answering scientific questions by deduction and described it as follows: “Having first determined the question according to his will, man then resorts to experience, and bending her to conformity with his placets, leads her about like a captive in a procession.”[9] Bacon wanted a method that relied on repeatable observations, or experiments. He was notably the first to order the scientific method as we understand it today.
There remains simple experience; which, if taken as it comes, is called accident, if sought for, experiment. The true method of experience first lights the candle [hypothesis], and then by means of the candle shows the way [arranges and delimits the experiment]; commencing as it does with experience duly ordered and digested, not bungling or erratic, and from it deducing axioms [theories], and from established axioms again new experiments.
– Francis Bacon. Novum Organum. 1620.[10]
When the problem or conditions do not permit a controlled experiment, such as in astronomical research, observational studies can be useful. For example, Tycho Brahe made careful observations and recorded measurements of stellar and planetary positions over time. After Brahe's death, his measurements proved useful in the development of Johannes Kepler’s laws of planetary motion, which offered a better fit than did Ptolemy's theory.
In the centuries that followed, important advances and discoveries were made by people who applied the scientific method in different areas. For example, Galileo Galilei was able to accurately measure time and experiment to make accurate measurements and conclusions about the speed of a falling body. Antoine Lavoisier was a French chemist in the late 1700s who used experiment to describe new areas such as combustion and biochemistry and to develop the theory of conservation of mass (matter).[11] During the 1800s, Louis Pasteur used the scientific method to disprove the prevailing theory of spontaneous generation and to develop the germ theory of disease.[12] Because of the importance of controlling potentially confounding variables, the use of well-designed laboratory experiments is preferred when possible.
[edit] Galileo Galilei
, where h is the height and g is the acceleration of gravity.Galileo Galilei (1564–1642) was a scientist who performed many quantitative experiments addressing many topics. Using several different methods, Galileo was able to accurately measure time. Previously, most scientists had used distance to describe falling bodies using geometry, which had been used and trusted since Euclid.[13] Galileo himself used geometrical methods to express his results. Galileo’s successes were aided by the development of a new mathematics as well as cleverly designed experiments and equipment. At that time, another kind of mathematics was being developed—algebra. Algebra allowed arithmetical calculations to become as sophisticated as geometric ones. Algebra also allowed the discoveries of scientists such as Galileo—as well as later scientists like Newton, Maxwell and Einstein—to be later summarized by mathematical equations. These equations described physical relationships in a precise, self-consistent manner.
One prominent example is the “ball and ramp experiment.”[14] In this experiment Galileo used an inclined plane and several steel balls of different weights. With this design, Galileo was able to slow down the falling motion and record, with reasonable accuracy, the times at which a steel ball passed certain markings on a beam.[15] Galileo disproved Aristotle’s assertion that weight affects the speed of an object’s fall. According to Aristotle’s Theory of Falling Bodies, the heavier steel ball would reach the ground before the lighter steel ball. Galileo’s hypothesis was that the two balls would reach the ground at the same time.
Other than Galileo, not many people of his day were able to accurately measure short time periods, such as the fall time of an object. Galileo accurately measured these short periods of time by creating a pulsilogon. This was a machine created to measure time using a pendulum.[16] The pendulum was synchronized to the human pulse. He used this to measure the time at which the weighted balls passed marks that he had made on the inclined plane. He measured to find that balls of different weights reached the bottom of the inclined plane at the same time and that the distance traveled was proportional to the square of the elapsed time.[17] Later scientists summarized Galileo’s results as The Equation of Falling Bodies.[18][19]
| Distance d traveled by an object falling for time t where g is gravitational acceleration (~ 9.8 m/s2): |  |
These results supported Galileo’s hypothesis that objects of different weights, when measured at the same point in their fall, fall at the same speed because they experience the same gravitational acceleration.
[edit] Antoine Lavoisier
Antoine Lavoisier (1743–1794) was a French chemist regarded as the founder of modern chemistry. Lavoisier's experiments were among the first truly quantitative chemical experiments. He showed that, although matter changes its state in a chemical reaction, the quantity of matter is the same at the end as at the beginning of every chemical reaction.[citation needed] In one experiment, he burned phosphorus and sulfur in air to see whether the results further supported his previous conclusion (Law of Conservation of Mass). In this experiment, however, he determined that the products weighed more than the original phosphorus and sulfur. He decided to do the experiment again. This time he measured the mass of the air surrounding the experiment as well. He discovered that the mass gained in the product was lost from the air. These experiments provided further support for his Law of Conservation of Mass.
One of Lavoisier’s experiments connected the worlds of respiration (physiology) and combustion. Lavoisier’s hypothesis was that combustion and respiration were one and the same, and combustion occurs with every instance of respiration. Lavoisier, working with Pierre-Simon Laplace, designed an ice calorimeter apparatus for measuring the amount of heat given off during combustion or respiration. This machine consisted of three concentric compartments. The center compartment held the source of heat, in this case, the guinea pig or piece of burning charcoal. The middle compartment held a specific amount of ice for the heat source to melt. The outside compartment contained packed snow for insulation. Lavoisier then measured the quantity of carbon dioxide and the quantity of heat produced by confining a live guinea pig in this apparatus. Lavoisier also measured the heat and carbon dioxide produced when burning a piece of charcoal in the calorimeter. Using this data, he concluded that respiration was in fact a slow combustion process. He also discovered through precise measurements that these processes produced carbon dioxide and heat with the same constant of proportionality. He found that for 224 grains of “fixed air” (CO2) produced, 13 oz. of ice was melted in the calorimeter. Converting grains to grams and using the energy required to melt 13 oz. of ice, one can compute that for each gram of CO2 produced, about 2.02 kcal of energy was produced by the combustion of carbon or by respiration in Lavoisier's calorimeter experiments. This compares well with the modern published heat of combustion for carbon of 2.13 kcal/g.[20] This continuous slow combustion, which Lavoisier and Laplace supposed took place in the lungs, enabled the living animal to maintain its body temperature above that of its surroundings, thus accounting for the puzzling phenomenon of animal heat.[21] Lavoisier concluded, “Lla respiration est donc une combustion," That is, respiratory gas exchange is combustion, like that of burning a candle.
Lavoisier was the first to conclude by experiment that the Law of Conservation of Mass applied to chemical change.[22] His hypothesis was that the mass of the reactants would be the same as the mass of the products in a chemical reaction. He experimented on vinous fermentation (biochemistry). He determined the amounts of hydrogen, oxygen, and carbon in sugar. He weighed a quantity of sugar, added yeast and water in measured amounts, and allowed the mixture to ferment. Lavoisier measured the mass of the carbonic acid gas and water that were given off during fermentation and weighed the residual liquor, the components of which were then separated and analyzed to determine their elementary composition.[23] In this way he controlled a couple of potential confounding factors. He was able to capture the carbonic acid gas and water vapor that were given off during fermentation so that his final measurements would be as accurate as possible. Lavoisier then concluded that the total mass of the reactants was equal to the mass of the final product and residue.[24] Moreover, he showed that the total mass of each constituent element before and after the chemical change remained the same. Similarly, he demonstrated via experimentation that the mass of products of combustion is equal to the mass of the reacting ingredients.
[edit] Louis Pasteur
Louis Pasteur (1822–1895), regarded as the “Father of Microbiological sciences and immunology,” was a French biologist during the 1800s.[25] He discovered and supported by experimental results the idea that disease-causing agents do not spontaneously appear but are alive and need the right environment to prosper and multiply. Stemming from this discovery, he used experiment to develop vaccines for chicken cholera, anthrax and rabies, and to develop methods for reducing bacteria in some food products by heating them (pasteurization). His work also led him to advocate (along with the English physician Dr. Joseph Lister) for antiseptic surgical techniques. Most scientists of that day believed that microscopic life sprang into existence from nonliving matter. This idea was called spontaneous generation.
Pasteur’s observations of tiny organisms under the microscope caused him to doubt spontaneous generation. He designed an experiment to test it. His hypothesis was that life could not arise from where there is no life. He took care to control possible confounding factors. For example, he needed to make sure there was no life, even microscopic, in the flasks of broth he used as a test medium. He decided to kill any microscopic organisms already present by boiling the broth until he was confident that any microorganisms present were killed. Pasteur also needed to make sure that no microscopic organisms entered the broth after boiling, yet the broth needed exposure to air to properly test the theory. A colleague suggested a flask with a neck the shape of an “S” turned sideways. Dust (which Pasteur thought contained microorganisms) would be trapped at the bottom of the first curve, but the air would flow freely through.[26]
Thus, if bacteria should really be spontaneously generated, then they should be growing in the flask after a few days. If spontaneous generation did not occur, then the contents of the flasks would remain lifeless. In the end, it was a complete success; not a single microorganism appeared in the broth. Then Pasteur allowed the dust containing the microorganisms to mix with the broth. In just a few days the broth became cloudy from millions of organisms growing in it. For two more years, he repeated the experiment in various conditions and locales to assure himself that the results were correct. In this way Pasteur supported his hypothesis that spontaneous generation does not occur.[27] Despite the experimental results supporting his hypotheses and his success curing or preventing various diseases, correcting the public misconception of spontaneous generation was a slow, difficult process.
As he worked to solve specific problems, Pasteur’s notions were sometimes corrected by the results of his experiments, such as when he was asked to find the cause of disease devastating the French silkworm industry in 1865. After a year of diligent work he correctly identified a culprit organism and gave practical advice for developing a healthy population of moths. However, when he tested his own advice, he found disease still present. It turned out he had been correct but incomplete – there were two organisms at work. It took two more years of experimenting to find the complete solution.[28]
[edit] Observational science
Observational science is used when it is impractical to fit a system into a laboratory setting. It can also be used when confounding factors are either limited or known well enough to analyze the data in light of them. In order for an observational science to be valid, the confounding factors must be known and accounted for.
[edit] Astronomy
An early European observational scientist was Tycho Brahe (1546–1601). Brahe’s observations of stellar and planetary positions were noteworthy both for their accuracy and quantity.[29] His celestial positions were much more accurate than those of any predecessor or contemporary. In an observatory funded for him by King Frederick II of Denmark, Brahe built some of the largest observing instruments yet constructed.[30] Because of the large size of this equipment, Brahe was able to measure angles to an accuracy of better than 0.1 degree.[31] This was more accurate than any previous observations and close to the limit that the human eye can observe.[31] In this way, Brahe was able to make observations about stellar and planetary positions in a lab setup.
Brahe himself was not a Copernican but proposed a system in which the Sun and Moon orbited the Earth, while the other planets orbited the Sun. His system provided a safe position for astronomers who were dissatisfied with older models but were reluctant to accept the Earth's motion. It gained a considerable following after 1616 when Rome decided officially that the heliocentric model was contrary to both philosophy and Scripture, and could be discussed only as a computational convenience that had no connection to fact. His system also offered a major innovation: while both the geocentric model and the heliocentric model as set forth by Copernicus relied on the idea of transparent rotating crystalline spheres to carry the planets in their orbits, Brahe eliminated the spheres entirely.
Johannes Kepler (1571–1630) used the accurate observations of Brahe to discover the shape of Mars’ orbit. His first hypothesis was that the orbit was circular. After four years of research and testing 70 different combinations of circles and epicycles, he devised a shape that would fit Mars’ orbit. However, the model was accurate to only 0.13 degrees.[32] Kepler knew that Brahe’s observations could be used to develop an orbit shape more accurate than this. Kepler eventually decided to try various oval shaped orbits. This implied that the speed of the planet changed as it traveled around the oval. After nine years, he found that elliptical orbits fit satisfactorily with the observed path of Mars. He found that this shape worked not only for Mars, but also for every planet that Brahe had observed.[32]
[edit] Biology
Observational studies are not experiments. By definition, observational studies lack the manipulation required for Baconian experiments. In addition, observational studies in biological systems often involve variables that are challenges to quantify or control. Nevertheless, observational studies are used because it is sometimes too difficult (too expensive, or too much time required) or unethical to conduct longitudinal experiments with human or animal subjects. In these situations, observational studies have value because they often suggest hypotheses that can be tested with randomized experiments or by collecting fresh data.
In providing therapies for human subjects, for example in psychology or health care, it is unethical to provide a substandard treatment to patients. Therefore, ethical review boards are supposed to stop clinical trials and other experiments unless a new treatment is believed to offer benefits as good as current best practice.[33] It is also unethical and often illegal to conduct randomized experiments on the effects of substandard or harmful treatments, such as the effects of ingesting arsenic on human health. To understand the effects of such exposures, scientists use observational studies.
Observational studies are limited because they lack the statistical properties of randomized experiments. In a randomized experiment, the method of randomization specified in the experimental protocol guides the statistical analysis, which is usually specified also by the experimental protocol.[34] Without a statistical model that reflects an objective randomization, the statistical analysis relies on a subjective model.[34] Inferences from subjective models are unreliable in theory and practice.[35] In fact, there are several cases where carefully conducted observational studies consistently give wrong results, that is, where the results of the observational studies are inconsistent and also differ from the results of experiments. For example, epidemiological studies of colon cancer consistently show beneficial correlations with broccoli consumption, while experiments find no benefit.[36]
A particular problem with observational studies involving human subjects is the great difficulty attaining fair comparisons between treatments (or exposures), because such studies are prone to selection bias, and groups receiving different treatments (exposures) may differ greatly according to their covariates (age, height, weight, medications, exercise, nutritional status, ethnicity, family medical history, etc.). In contrast, randomization implies that for each covariate, the mean for each group is expected to be the same. For any randomized trial, some variation from the mean is expected, of course, but the randomization ensures that the experimental groups have mean values that are close, due to the central limit theorem and Markov's inequality. With poor randomization, the systematic variation in covariates between the treatment groups (or exposure groups) makes it difficult to separate the effect of the treatment (exposure) from the effects of the other covariates, most of which have not been measured. The mathematical models used to analyze such data must consider each differing covariate (if measured), and the results will not be meaningful if a covariate is neither randomized nor included in the model.
To avoid these conditions that render an experiment far less useful, physicians conducting medical trials (such as for Food and Drug Administration approval), will quantify and randomize the covariates that can be identified. Researchers attempt to reduce the biases of observational studies with complicated statistical methods such as propensity score matching methods, which require large populations of subjects and extensive information on covariates. Outcomes are also quantified when possible (bone density, amount of some cell or substance in the blood, physical strength or endurance, etc.) and not based on a subject's or a professional observer's opinion. In this way, the design of an observational study can render the results more objective and therefore more convincing.
See also hierarchy of evidence and quasi-empirical methods.
Scientific Career Albert Einstein
Throughout his life, Einstein published hundreds of books and articles. Most were about physics, but a few expressed leftist political opinions about pacifism, socialism, and zionism.[4][7] In addition to the work he did by himself he also collaborated with other scientists on additional projects including the Bose–Einstein statistics, the Einstein refrigerator and others.[42]
Physics in 1900
Einstein’s early papers all come from attempts to demonstrate that atoms exist and have a finite nonzero size. At the time of his first paper in 1902, it was not yet completely accepted by physicists that atoms were real, even though chemists had good evidence ever since Antoine Lavoisier’s work a century earlier. The reason physicists were skeptical was because no 19th century theory could fully explain the properties of matter from the properties of atoms.
Ludwig Boltzmann was a leading 19th century atomist physicist, who had struggled for years to gain acceptance for atoms. Boltzmann had given an interpretation of the laws of thermodynamics, suggesting that the law of entropy increase is statistical. In Boltzmann’s way of thinking, the entropy is the logarithm of the number of ways a system could be configured inside. The reason the entropy goes up is only because it is more likely for a system to go from a special state with only a few possible internal configurations to a more generic state with many. While Boltzmann’s statistical interpretation of entropy is universally accepted today, and Einstein believed it, at the turn of the 20th century it was a minority position.
The statistical idea was most successful in explaining the properties of gases. James Clerk Maxwell, another leading atomist, had found the distribution of velocities of atoms in a gas, and derived the surprising result that the viscosity of a gas should be independent of density. Intuitively, the friction in a gas would seem to go to zero as the density goes to zero, but this is not so, because the mean free path of atoms becomes large at low densities. A subsequent experiment by Maxwell and his wife confirmed this surprising prediction. Other experiments on gases and vacuum, using a rotating slitted drum, showed that atoms in a gas had velocities distributed according to Maxwell’s distribution law.
In addition to these successes, there were also inconsistencies. Maxwell noted that at cold temperatures, atomic theory predicted specific heats that are too large. In classical statistical mechanics, every spring-like motion has thermal energy kBT on average at temperature T, so that the specific heat of every spring is Boltzmann’s constant kB. A monatomic solid with N atoms can be thought of as N little balls representing N atoms attached to each other in a box grid with 3N springs, so the specific heat of every solid is 3NkB, a result which became known as the Dulong–Petit law. This law is true at room temperature, but not for colder temperatures. At temperatures near zero, the specific heat goes to zero.
Similarly, a gas made up of a molecule with two atoms can be thought of as two balls on a spring. This spring has energy kBT at high temperatures, and should contribute an extra kB to the specific heat. It does at temperatures of about 1000 degrees, but at lower temperature, this contribution disappears. At zero temperature, all other contributions to the specific heat from rotations and vibrations also disappear. This behavior was inconsistent with classical physics.
The most glaring inconsistency was in the theory of light waves. Continuous waves in a box can be thought of as infinitely many spring-like motions, one for each possible standing wave. Each standing wave has a specific heat of kB, so the total specific heat of a continuous wave like light should be infinite in classical mechanics. This is obviously wrong, because it would mean that all energy in the universe would be instantly sucked up into light waves, and everything would slow down and stop.
These inconsistencies led some people to say that atoms were not physical, but mathematical. Notable among the skeptics was Ernst Mach, whose positivist philosophy led him to demand that if atoms are real, it should be possible to see them directly.[43] Mach believed that atoms were a useful fiction, that in reality they could be assumed to be infinitesimally small, that Avogadro’s number was infinite, or so large that it might as well be infinite, and kB was infinitesimally small. Certain experiments could then be explained by atomic theory, but other experiments could not, and this is the way it will always be.
Einstein opposed this position. Throughout his career, he was a realist. He believed that a single consistent theory should explain all observations, and that this theory would be a description of what was really going on, underneath it all. So he set out to show that the atomic point of view was correct. This led him first to thermodynamics, then to statistical physics, and to the theory of specific heats of solids.
In 1905, while he was working in the patent office, the leading German language physics journal Annalen der Physik published four of Einstein’s papers. The four papers eventually were recognized as revolutionary, and 1905 became known as Einstein’s "Miracle Year", and the papers as the Annus Mirabilis Papers.
Thermodynamic fluctuations and statistical physics
Einstein’s earliest papers were concerned with thermodynamics. He wrote a paper establishing a thermodynamic identity in 1902, and a few other papers which attempted to interpret phenomena from a statistical atomic point of view.
His research in 1903 and 1904 was mainly concerned with the effect of finite atomic size on diffusion phenomena. As in Maxwell’s work, the finite nonzero size of atoms leads to effects which can be observed. This research, and the thermodynamic identity, were well within the mainstream of physics in his time. They would eventually form the content of his PhD thesis.[45]
His first major result in this field was the theory of thermodynamic fluctuations. When in equilibrium, a system has a maximum entropy and, according to the statistical interpretation, it can fluctuate a little bit. Einstein pointed out that the statistical fluctuations of a macroscopic object, like a mirror suspended on spring, would be completely determined by the second derivative of the entropy with respect to the position of the mirror.
Searching for ways to test this relation, his great breakthrough came in 1905. The theory of fluctuations, he realized, would have a visible effect for an object which could move around freely. Such an object would have a velocity which is random, and would move around randomly, just like an individual atom. The average kinetic energy of the object would be kBT, and the time decay of the fluctuations would be entirely determined by the law of friction.
The law of friction for a small ball in a viscous fluid like water was discovered by George Stokes. He showed that for small velocities, the friction force would be proportional to the velocity, and to the radius of the particle (see Stokes’ law). This relation could be used to calculate how far a small ball in water would travel due to its random thermal motion, and Einstein noted that such a ball, of size about a micron, would travel about a few microns per second. This motion could be easily detected with a microscope and indeed, as Brownian motion, had actually been observed by the botanist Robert Brown. Einstein was able to identify this motion with that predicted by his theory. Since the fluctuations which give rise to Brownian motion are just the same as the fluctuations of the velocities of atoms, measuring the precise amount of Brownian motion using Einstein’s theory would show that Boltzmann’s constant is non-zero and would measure Avogadro’s number.
These experiments were carried out a few years later by Jean Baptiste Perrin, and gave a rough estimate of Avogadro’s number consistent with the more accurate estimates due to Max Planck’s theory of blackbody light and Robert Millikan’s measurement of the charge of the electron.[46] Unlike the other methods, Einstein’s required very few theoretical assumptions or new physics, since it was directly measuring atomic motion on visible grains.
Einstein’s theory of Brownian motion was the first paper in the field of statistical physics. It established that thermodynamic fluctuations were related to dissipation. This was shown by Einstein to be true for time-independent fluctuations, but in the Brownian motion paper he showed that dynamical relaxation rates calculated from classical mechanics could be used as statistical relaxation rates to derive dynamical diffusion laws. These relations are known as Einstein relations.
The theory of Brownian motion was the least revolutionary of Einstein’s Annus mirabilis papers, but it is the most frequently cited, and had an important role in securing the acceptance of the atomic theory by physicists.
Thought experiments and a-priori physical principles
Einstein’s thinking underwent a transformation in 1905. He had come to understand that quantum properties of light mean that Maxwell’s equations were only an approximation. He knew that new laws would have to replace these, but he did not know how to go about finding those laws. He felt that guessing formal relations would not go anywhere.
So he decided to focus on a-priori principles instead, which are statements about physical laws which can be understood to hold in a very broad sense even in domains where they have not yet been shown to apply. A well accepted example of an a-priori principle is rotational invariance. If a new force is discovered in physics, it is assumed to be rotationally invariant almost automatically, without thought. Einstein sought new principles of this sort, to guide the production of physical ideas. Once enough principles are found, then the new physics will be the simplest theory consistent with the principles and with previously known laws.
The first general a-priori principle he found was the principle of relativity, that uniform motion is indistinguishable from rest. This was understood by Hermann Minkowski to be a generalization of rotational invariance from space to space-time. Other principles postulated by Einstein and later vindicated are the principle of equivalence and the principle of adiabatic invariance of the quantum number. Another of Einstein’s general principles, Mach’s principle, is fiercely debated, and whether it holds in our world or not is still not definitively established.
The use of a-priori principles is a distinctive unique signature of Einstein’s early work, and has become a standard tool in modern theoretical physics.
Special relativity
His 1905 paper on the electrodynamics of moving bodies introduced his theory of special relativity, which showed that the observed independence of the speed of light on the observer’s state of motion required fundamental changes to the notion of simultaneity. Consequences of this include the time-space frame of a moving body slowing down and contracting (in the direction of motion) relative to the frame of the observer. This paper also argued that the idea of a luminiferous aether – one of the leading theoretical entities in physics at the time – was superfluous.[47] In his paper on mass–energy equivalence, which had previously been considered to be distinct concepts, Einstein deduced from his equations of special relativity what has been called the twentieth century’s best-known equation: E = mc2.[48][49] This equation suggests that tiny amounts of mass could be converted into huge amounts of energy and presaged the development of nuclear power.[50] Einstein’s 1905 work on relativity remained controversial for many years, but was accepted by leading physicists, starting with Max Planck.[51][52]
Photons
In a 1905 paper,[53] Einstein postulated that light itself consists of localized particles (quanta). Einstein’s light quanta were nearly universally rejected by all physicists, including Max Planck and Niels Bohr. This idea only became universally accepted in 1919, with Robert Millikan’s detailed experiments on the photoelectric effect, and with the measurement of Compton scattering.
Einstein’s paper on the light particles was almost entirely motivated by thermodynamic considerations. He was not at all motivated by the detailed experiments on the photoelectric effect, which did not confirm his theory until fifteen years later. Einstein considers the entropy of light at temperature T, and decomposes it into a low-frequency part and a high-frequency part. The high-frequency part, where the light is described by Wien’s law, has an entropy which looks exactly the same as the entropy of a gas of classical particles.
Since the entropy is the logarithm of the number of possible states, Einstein concludes that the number of states of short wavelength light waves in a box with volume V is equal to the number of states of a group of localizable particles in the same box. Since (unlike others) he was comfortable with the statistical interpretation, he confidently postulates that the light itself is made up of localized particles, as this is the only reasonable interpretation of the entropy.
This leads him to conclude that each wave of frequency f is associated with a collection of photons with energy hf each, where h is Planck’s constant. He does not say much more, because he is not sure how the particles are related to the wave. But he does suggest that this idea would explain certain experimental results, notably the photoelectric effect.[54]
Quantized atomic vibrations
Einstein continued his work on quantum mechanics in 1906, by explaining the specific heat anomaly in solids. This was the first application of quantum theory to a mechanical system. Since Planck’s distribution for light oscillators had no problem with infinite specific heats, the same idea could be applied to solids to fix the specific heat problem there. Einstein showed in a simple model that the hypothesis that solid motion is quantized explains why the specific heat of a solid goes to zero at zero temperature.
Einstein’s model treats each atom as connected to a single spring. Instead of connecting all the atoms to each other, which leads to standing waves with all sorts of different frequencies, Einstein imagined that each atom was attached to a fixed point in space by a spring. This is not physically correct, but it still predicts that the specific heat is 3NkB, since the number of independent oscillations stays the same.
Einstein then assumes that the motion in this model is quantized, according to the Planck law, so that each independent spring motion has energy which is an integer multiple of hf, where f is the frequency of oscillation. With this assumption, he applied Boltzmann’s statistical method to calculate the average energy of the spring. The result was the same as the one that Planck had derived for light: for temperatures where kBT is much smaller than hf, the motion is frozen, and the specific heat goes to zero.
So Einstein concluded that quantum mechanics would solve the main problem of classical physics, the specific heat anomaly. The particles of sound implied by this formulation are now called phonons. Because all of Einstein’s springs have the same stiffness, they all freeze out at the same temperature, and this leads to a prediction that the specific heat should go to zero exponentially fast when the temperature is low. The solution to this problem is to solve for the independent normal modes individually, and to quantize those. Then each normal mode has a different frequency, and long wavelength vibration modes freeze out at colder temperatures than short wavelength ones. This was done by Debye, and after this modification Einstein’s quantization method reproduced quantitatively the behavior of the specific heats of solids at low temperatures.
This work was the foundation of condensed matter physics.
Adiabatic principle and action-angle variables
Throughout the 1910s, quantum mechanics expanded in scope to cover many different systems. After Ernest Rutherford discovered the nucleus and proposed that electrons orbit like planets, Niels Bohr was able to show that the same quantum mechanical postulates introduced by Planck and developed by Einstein would explain the discrete motion of electrons in atoms, and the periodic table of the elements.
Einstein contributed to these developments by linking them with the 1898 arguments Wilhelm Wien had made. Wien had shown that the hypothesis of adiabatic invariance of a thermal equilibrium state allows all the blackbody curves at different temperature to be derived from one another by a simple shifting process. Einstein noted in 1911 that the same adiabatic principle shows that the quantity which is quantized in any mechanical motion must be an adiabatic invariant. Arnold Sommerfeld identified this adiabatic invariant as the action variable of classical mechanics. The law that the action variable is quantized was the basic principle of the quantum theory as it was known between 1900 and 1925.
Wave-particle duality
Although the patent office promoted Einstein to Technical Examiner Second Class in 1906, he had not given up on academia. In 1908, he became a privatdozent at the University of Bern.[55] In "über die Entwicklung unserer Anschauungen über das Wesen und die Konstitution der Strahlung" ("The Development of Our Views on the Composition and Essence of Radiation"), on the quantization of light, and in an earlier 1909 paper, Einstein showed that Max Planck’s energy quanta must have well-defined momenta and act in some respects as independent, point-like particles. This paper introduced the photon concept (although the name photon was introduced later by Gilbert N. Lewis in 1926) and inspired the notion of wave-particle duality in quantum mechanics.
Theory of critical opalescence
Einstein returned to the problem of thermodynamic fluctuations, giving a treatment of the density variations in a fluid at its critical point. Ordinarily the density fluctuations are controlled by the second derivative of the free energy with respect to the density. At the critical point, this derivative is zero, leading to large fluctuations. The effect of density fluctuations is that light of all wavelengths is scattered, making the fluid look milky white. Einstein relates this to Raleigh scattering, which is what happens when the fluctuation size is much smaller than the wavelength, and which explains why the sky is blue.[56]
Zero-point energy
Einstein’s physical intuition led him to note that Planck’s oscillator energies had an incorrect zero point. He modified Planck’s hypothesis by stating that the lowest energy state of an oscillator is equal to 1⁄2hf, to half the energy spacing between levels. This argument, which was made in 1913 in collaboration with Otto Stern, was based on the thermodynamics of a diatomic molecule which can split apart into two free atoms.
Principle of equivalence
In 1907, while still working at the patent office, Einstein had what he would call his "happiest thought". He realized that the principle of relativity could be extended to gravitational fields. He thought about the case of a uniformly accelerated box not in a gravitational field, and noted that it would be indistinguishable from a box sitting still in an unchanging gravitational field.[57] He used special relativity to see that the rate of clocks at the top of a box accelerating upward would be faster than the rate of clocks at the bottom. He concludes that the rates of clocks depend on their position in a gravitational field, and that the difference in rate is proportional to the gravitational potential to first approximation.
Although this approximation is crude, it allowed him to calculate the deflection of light by gravity, and show that it is nonzero. This gave him confidence that the scalar theory of gravity proposed by Gunnar Nordström was incorrect. But the actual value for the deflection that he calculated was too small by a factor of two, because the approximation he used doesn’t work well for things moving at near the speed of light. When Einstein finished the full theory of general relativity, he would rectify this error and predict the correct amount of light deflection by the sun.
From Prague, Einstein published a paper about the effects of gravity on light, specifically the gravitational redshift and the gravitational deflection of light. The paper challenged astronomers to detect the deflection during a solar eclipse.[58] German astronomer Erwin Finlay-Freundlich publicized Einstein’s challenge to scientists around the world.[59]
Einstein thought about the nature of the gravitational field in the years 1909–1912, studying its properties by means of simple thought experiments. A notable one is the rotating disk. Einstein imagined an observer making experiments on a rotating turntable. He noted that such an observer would find a different value for the mathematical constant pi than the one predicted by Euclidean geometry. The reason is that the radius of a circle would be measured with an uncontracted ruler, but, according to special relativity, the circumference would seem to be longer because the ruler would be contracted.
Since Einstein believed that the laws of physics were local, described by local fields, he concluded from this that spacetime could be locally curved. This led him to study Riemannian geometry, and to formulate general relativity in this language.
Hole argument and Entwurf theory
While developing general relativity, Einstein became confused about the gauge invariance in the theory. He formulated an argument that led him to conclude that a general relativistic field theory is impossible. He gave up looking for fully generally covariant tensor equations, and searched for equations that would be invariant under general linear transformations only.
The Entwurf ("draft") theory was the result of these investigations. As its name suggests, it was a sketch of a theory, with the equations of motion supplemented by additional gauge fixing conditions. Simultaneously less elegant and more difficult than general relativity, Einstein abandoned the theory after realizing that the hole argument was mistaken.
General relativity
In 1912, Einstein returned to Switzerland to accept a professorship at his alma mater, the ETH. Once back in Zurich, he immediately visited his old ETH classmate Marcel Grossmann, now a professor of mathematics, who introduced him to Riemannian geometry and, more generally, to differential geometry. On the recommendation of Italian mathematician Tullio Levi-Civita, Einstein began exploring the usefulness of general covariance (essentially the use of tensors) for his gravitational theory. For a while Einstein thought that there were problems with the approach, but he later returned to it and, by late 1915, had published his general theory of relativity in the form in which it is used today.[60] This theory explains gravitation as distortion of the structure of spacetime by matter, affecting the inertial motion of other matter. During World War I, the work of Central Powers scientists was available only to Central Powers academics, for national security reasons. Some of Einstein’s work did reach the United Kingdom and the United States through the efforts of the Austrian Paul Ehrenfest and physicists in the Netherlands, especially 1902 Nobel Prize-winner Hendrik Lorentz and Willem de Sitter of Leiden University. After the war ended, Einstein maintained his relationship with Leiden University, accepting a contract as an Extraordinary Professor; for ten years, from 1920 to 1930, he travelled to Holland regularly to lecture.[61]
In 1917, several astronomers accepted Einstein ’s 1911 challenge from Prague. The Mount Wilson Observatory in California, U.S., published a solar spectroscopic analysis that showed no gravitational redshift.[62] In 1918, the Lick Observatory, also in California, announced that it too had disproved Einstein’s prediction, although its findings were not published.[63]
However, in May 1919, a team led by the British astronomer Arthur Stanley Eddington claimed to have confirmed Einstein’s prediction of gravitational deflection of starlight by the Sun while photographing a solar eclipse with dual expeditions in Sobral, northern Brazil, and Príncipe, a west African island.[59] Nobel laureate Max Born praised general relativity as the "greatest feat of human thinking about nature";[65] fellow laureate Paul Dirac was quoted saying it was "probably the greatest scientific discovery ever made".[66] The international media guaranteed Einstein’s global renown.
There have been claims that scrutiny of the specific photographs taken on the Eddington expedition showed the experimental uncertainty to be comparable to the same magnitude as the effect Eddington claimed to have demonstrated, and that a 1962 British expedition concluded that the method was inherently unreliable.[64] The deflection of light during a solar eclipse was confirmed by later, more accurate observations.[67] Some resented the newcomer’s fame, notably among some German physicists, who later started the Deutsche Physik (German Physics) movement.[68][69]
Cosmology
In 1917, Einstein applied the General theory of relativity to model the structure of the universe as a whole. He wanted the universe to be eternal and unchanging, but this type of universe is not consistent with relativity. To fix this, Einstein modified the general theory by introducing a new notion, the cosmological constant. With a positive cosmological constant, the universe could be an eternal static sphere[70]
Einstein believed a spherical static universe is philosophically preferred, because it would obey Mach’s principle. He had shown that general relativity incorporates Mach’s principle to a certain extent in frame dragging by gravitomagnetic fields, but he knew that Mach’s idea would not work if space goes on forever. In a closed universe, he believed that Mach’s principle would hold.
Mach’s principle has generated much controversy over the years.
Modern quantum theory
In 1917, at the height of his work on relativity, Einstein published an article in Physikalische Zeitschrift that proposed the possibility of stimulated emission, the physical process that makes possible the maser and the laser.[73] This article showed that the statistics of absorption and emission of light would only be consistent with Planck’s distribution law if the emission of light into a mode with n photons would be enhanced statistically compared to the emission of light into an empty mode. This paper was enormously influential in the later development of quantum mechanics, because it was the first paper to show that the statistics of atomic transitions had simple laws. Einstein discovered Louis de Broglie’s work, and supported his ideas, which were received skeptically at first. In another major paper from this era, Einstein gave a wave equation for de Broglie waves, which Einstein suggested was the Hamilton–Jacobi equation of mechanics. This paper would inspire Schrödinger’s work of 1926.
Bose–Einstein statistics
In 1924, Einstein received a description of a statistical model from Indian physicist Satyendra Nath Bose, based on a counting method that assumed that light could be understood as a gas of indistinguishable particles. Einstein noted that Bose’s statistics applied to some atoms as well as to the proposed light particles, and submitted his translation of Bose’s paper to the Zeitschrift für Physik. Einstein also published his own articles describing the model and its implications, among them the Bose–Einstein condensate phenomenon that some particulates should appear at very low temperatures.[74] It was not until 1995 that the first such condensate was produced experimentally by Eric Allin Cornell and Carl Wieman using ultra-cooling equipment built at the NIST–JILA laboratory at the University of Colorado at Boulder.[75] Bose–Einstein statistics are now used to describe the behaviors of any assembly of bosons. Einstein’s sketches for this project may be seen in the Einstein Archive in the library of the Leiden University.[42]
Energy momentum pseudotensor
General relativity includes a dynamical spacetime, so it is difficult to see how to identify the conserved energy and momentum. Noether’s theorem allows these quantities to be determined from a Lagrangian with translation invariance, but general covariance makes translation invariance into something of a gauge symmetry. The energy and momentum derived within general relativity by Noether’s presecriptions do not make a real tensor for this reason.
Einstein argued that this is true for fundamental reasons, because the gravitational field could be made to vanish by a choice of coordinates. He maintained that the non-covariant energy momentum pseudotensor was in fact the best description of the energy momentum distribution in a gravitational field. This approach has been echoed by Lev Landau and Evgeny Lifshitz, and others, and has become standard.
The use of non-covariant objects like pseudotensors was heavily criticized in 1917 by Erwin Schrödinger and others.
Unified field theory
Following his research on general relativity, Einstein entered into a series of attempts to generalize his geometric theory of gravitation, which would allow the explanation of electromagnetism. In 1950, he described his "unified field theory" in a Scientific American article entitled "On the Generalized Theory of Gravitation." [76] Although he continued to be lauded for his work, Einstein became increasingly isolated in his research, and his efforts were ultimately unsuccessful. In his pursuit of a unification of the fundamental forces, Einstein ignored some mainstream developments in physics, most notably the strong and weak nuclear forces, which were not well understood until many years after his death. Mainstream physics, in turn, largely ignored Einstein’s approaches to unification. Einstein’s dream of unifying other laws of physics with gravity motivates modern quests for a theory of everything and in particular string theory, where geometrical fields emerge in a unified quantum-mechanical setting.
Wormholes
Einstein collaborated with others to produce a model of a wormhole. His motivation was to model elementary particles with charge as a solution of gravitational field equations, in line with the program outlined in the paper "Do Gravitational Fields play an Important Role in the Constitution of the Elementary Particles?". These solutions cut and pasted Schwarzschild black holes to make a bridge between two patches.
If one end of a wormhole was positively charged, the other end would be negatively charged. These properties led Einstein to believe that pairs of particles and antiparticles could be described in this way.
Einstein–Cartan theory
In order to incorporate spinning point particles into general relativity, the affine connection needed to be generalized to include an antisymmetric part, called the torsion. This modification was made by Einstein and Cartan in the 1920s.
Einstein–Podolsky–Rosen paradox
In 1935, Einstein returned to the question of quantum mechanics. He considered how a measurement on one of two entangled particles would affect the other. He noted, along with his collaborators, that by performing different measurements on the distant particle, either of position or momentum, different properties of the entangled partner could be discovered without disturbing it in any way.
He then used a hypothesis of local realism to conclude that the other particle had these properties already determined. The principle he proposed is that if it is possible to determine what the answer to a position or momentum measurement would be, without in any way disturbing the particle, then the particle actually has values of position or momentum.
This principle distilled the essence of Einstein’s objection to quantum mechanics. As a physical principle, it has since been shown to be incompatible with experiments.
Equations of motion
The theory of general relativity has two fundamental laws – the Einstein equations which describe how space curves, and the geodesic equation which describes how particles move.
Since the equations of general relativity are non-linear, a lump of energy made out of pure gravitational fields, like a black hole, would move on a trajectory which is determined by the Einstein equations themselves, not by a new law. So Einstein proposed that the path of a singular solution, like a black hole, would be determined to be a geodesic from general relativity itself.
This was established by Einstein, Infeld and Hoffmann for pointlike objects without angular momentum, and by Roy Kerr for spinning objects.
Einstein’s controversial beliefs in physics
In addition to his well-accepted results, some of Einstein’s views are regarded as controversial:
- In the special relativity paper (in 1905), Einstein noted that, given a specific definition of the word "force" (a definition which he later agreed was not advantageous), and if we choose to maintain (by convention) the equation mass x acceleration = force, then one arrives at
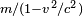as the expression for the transverse mass of a fast moving particle. This differs from the accepted expression today, because, as noted in the footnotes to Einstein's paper added in the 1913 reprint, "it is more to the point to define force in such a way that the laws of energy and momentum assume the simplest form", as was done, for example, by Max Planck in 1906, who gave the now familiar expression 
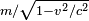for the transverse mass. As Miller points out, this is equivalent to the transverse mass predictions of both Einstein and Lorentz. Einstein had commented already in the 1905 paper that "With a different definition of force and acceleration, we should naturally obtain other expressions for the masses. This shows that in comparing different theories... we must proceed very cautiously." [77] - Einstein published (in 1922) a qualitative theory of superconductivity based on the vague idea of electrons shared in orbits. This paper predated modern quantum mechanics, and today is regarded as being incorrect. The current theory of low temperature superconductivity was only worked out in 1957, thirty years after the establishing of modern quantum mechanics. However, even today, superconductivity is not well understood, and alternative theories continue to be put forward, especially to account for high-temperature superconductors.[citation needed]
- After introducing the concept of gravitational waves in 1917, Einstein subsequently entertained doubts about whether they could be physically realized. In 1937 he published a paper saying that the focusing properties of geodesics in general relativity would lead to an instability which causes plane gravitational waves to collapse in on themselves. While this is true to a certain extent in some limits, because gravitational instabilities can lead to a concentration of energy density into black holes, for plane waves of the type Einstein and Rosen considered in their paper, the instabilities are under control. Einstein retracted this position a short time later.[citation needed]
- Einstein denied several times that black holes could form. In 1939 he published a paper that argues that a star collapsing would spin faster and faster, spinning at the speed of light with infinite energy well before the point where it is about to collapse into a black hole. This paper received no citations, and the conclusions are well understood to be wrong. Einstein’s argument itself is inconclusive, since he only shows that stable spinning objects have to spin faster and faster to stay stable before the point where they collapse. But it is well understood today (and was understood well by some even then) that collapse cannot happen through stationary states the way Einstein imagined. Nevertheless, the extent to which the models of black holes in classical general relativity correspond to physical reality remains unclear, and in particular the implications of the central singularity implicit in these models are still not understood. Efforts to conclusively prove the existence of event horizons have still not been successful, and most scientists acknowledge that no such proof is even possible.[citation needed]
- Closely related to his rejection of black holes, Einstein believed that the exclusion of singularities might restrict the class of solutions of the field equations so as to force solutions compatible with quantum mechanics, but no such theory has ever been found.[citation needed]
- In the early days of quantum mechanics, Einstein tried to show that the uncertainty principle was not valid, but by 1927 he had become convinced that it was valid.[citation needed]
- In the EPR paper, Einstein argued that quantum mechanics cannot be a complete realistic and local representation of phenomena, given specific definitions of "realism", "locality", and "completeness". The modern consensus is that Einstein's concept of realism is too restrictive.[citation needed]
- Einstein himself considered the introduction of the cosmological term in his 1917 paper founding cosmology as a "blunder".[78] The theory of general relativity predicted an expanding or contracting universe, but Einstein wanted a universe which is an unchanging three dimensional sphere, like the surface of a three dimensional ball in four dimensions. He wanted this for philosophical reasons, so as to incorporate Mach’s principle in a reasonable way. He stabilized his solution by introducing a cosmological constant, and when the universe was shown to be expanding, he retracted the constant as a blunder. This is not really much of a blunder – the cosmological constant is necessary within general relativity as it is currently understood, and it is widely believed to have a nonzero value today.
- Einstein did not immediately appreciate the value of Minkowski's four-dimensional formulation of special relativity, although within a few years he had adopted it as the basis for his theory of gravitation.[citation needed]
- Finding it too formal, Einstein believed that Heisenberg’s matrix mechanics was incorrect. He changed his mind when Schrödinger and others demonstrated that the formulation in terms of the Schrödinger equation, based on Einstein’s wave-particle duality was equivalent to Heisenberg’s matrices.[citation needed]
Collaboration with other scientists
In addition to long time collaborators Leopold Infeld, Nathan Rosen, Peter Bergmann and others, Einstein also had some one-shot collaborations with various scientists.
Einstein-de Haas experiment
Einstein and De Haas demonstrated that magnetization is due to the motion of electrons, nowadays known to be the spin. In order to show this, they reversed the magnetization in an iron bar suspended on a torsion pendulum. They confirmed that this leads the bar to rotate, because the electron’s angular momentum changes as the magnetization changes. This experiment needed to be sensitive, because the angular momentum associated with electrons is small, but it definitively established that electron motion of some kind is responsible for magnetization.
Schrödinger gas model
Einstein suggested to Erwin Schrödinger that he might be able to reproduce the statistics of a Bose–Einstein gas by considering a box. Then to each possible quantum motion of a particle in a box associate an independent harmonic oscillator. Quantizing these oscillators, each level will have an integer occupation number, which will be the number of particles in it.
This formulation is a form of second quantization, but it predates modern quantum mechanics. Erwin Schrödinger applied this to derive the thermodynamic properties of a semiclassical ideal gas. Schrödinger urged Einstein to add his name as co-author, although Einstein declined the invitation.[79]
Einstein refrigerator
In 1926, Einstein and his former student Leó Szilárd co-invented (and in 1930, patented) the Einstein refrigerator. This Absorption refrigerator was then revolutionary for having no moving parts and using only heat as an input.[80] On 11 November 1930, U.S. Patent 1,781,541 was awarded to Albert Einstein and Leó Szilárd for the refrigerator. Their invention was not immediately put into commercial production, as the most promising of their patents were quickly bought up by the Swedish company Electrolux to protect its refrigeration technology from competition.[81]
Bohr versus Einstein
In the 1920s, quantum mechanics developed into a more complete theory. Einstein was unhappy with the Copenhagen interpretation of quantum theory developed by Niels Bohr and Werner Heisenberg. In this interpretation, quantum phenomena are inherently probabilistic, with definite states resulting only upon interaction with classical systems. A public debate between Einstein and Bohr followed, lasting on and off for many years (including during the Solvay Conferences). Einstein formulated thought experiments against the Copenhagen interpretation, which were all rebutted by Bohr. In a 1926 letter to Max Born, Einstein wrote: "I, at any rate, am convinced that He [God] does not throw dice." [82]
Einstein was never satisfied by what he perceived to be quantum theory’s intrinsically incomplete description of nature, and in 1935 he further explored the issue in collaboration with Boris Podolsky and Nathan Rosen, noting that the theory seems to require non-local interactions; this is known as the EPR paradox.[83] The EPR experiment has since been performed, with results confirming quantum theory’s predictions.[84] Repercussions of the Einstein–Bohr debate have found their way into philosophical discourse.
